Burger’s Equation Discontinuity and Physics-Informed Neural Networks: A Revolutionary Approach in Computational Physics

In the realm of computational physics, solving complex partial differential equations (PDEs) is a key challenge, especially when these equations exhibit discontinuities or sharp gradients. One such classic equation is the Burger’s equation, which models a wide variety of physical phenomena, from fluid dynamics to traffic flow. While traditional numerical methods struggle with handling discontinuities in Burger’s equation, Physics-Informed Neural Networks (PINNs) have emerged as a promising solution, blending the power of neural networks with the laws of physics to accurately solve these types of equations.

In this article, we will explore the fundamentals of Burger’s equation, the challenges posed by discontinuities, and how Physics-Informed Neural Networks offer an innovative approach to overcoming these challenges.

What is Burger’s Equation?

Burger’s equation is a fundamental PDE that describes various physical systems, often representing the behavior of shock waves and turbulence. Its standard form is:

∂u∂t+u∂u∂x=ν∂2u∂x2\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = \nu \frac{\partial^2 u}{\partial x^2}∂t∂u​+u∂x∂u​=ν∂x2∂2u​

where:

• $u(x,t)$ is the unknown function (typically the velocity field of a fluid),
• $\nu$ is the viscosity (a parameter that controls the diffusion),
• $x$ and $t$ represent space and time, respectively.

The equation combines nonlinear advection (represented by the u∂u∂xu \frac{\partial u}{\partial x}u∂x∂u​ term) with a diffusion term (ν∂2u∂x2\nu \frac{\partial^2 u}{\partial x^2}ν∂x2∂2u​), leading to rich phenomena such as shock formation, boundary layers, and smooth fluid flows. In the presence of shock waves, where steep gradients and discontinuities appear, solving this equation numerically becomes increasingly difficult.

Challenges of Discontinuity in Burger’s Equation

Discontinuities arise in Burger’s equation when the nonlinearity in the advection term leads to the formation of shock waves — regions where the solution experiences a sudden change in value over a very small distance. These shock waves are essential to many real-world applications, such as fluid dynamics, traffic modeling, and acoustics, but they pose significant challenges for traditional numerical methods, including finite difference methods and finite element methods.

The key issues include:

• Numerical instability: Traditional methods often fail to maintain the sharpness of the discontinuity, leading to numerical smearing or oscillations.
• Loss of accuracy: Methods like central differencing or explicit solvers tend to produce inaccurate approximations in the presence of steep gradients or shocks.
• Difficulty in handling sharp transitions: The steep gradients in shock regions demand highly refined meshes, which can lead to expensive computations, especially for large-scale problems.

Physics-Informed Neural Networks (PINNs): A New Frontier

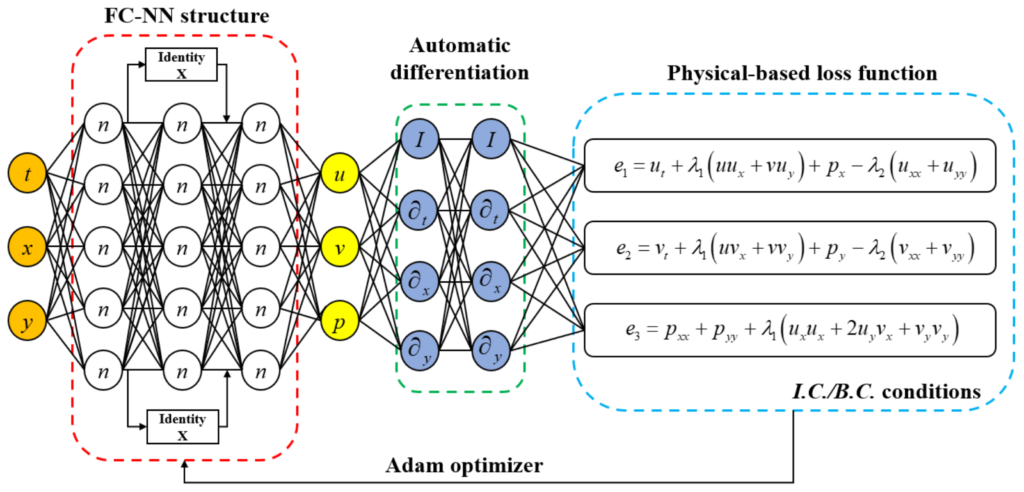
Physics-Informed Neural Networks (PINNs) represent a breakthrough in solving PDEs by integrating the principles of physics directly into the training of deep learning models. Instead of relying solely on data, PINNs incorporate known physical laws — such as Burger’s equation — as part of the neural network’s objective function, ensuring that the solution adheres to these laws even in regions of discontinuity.

How PINNs Work

A PINN for solving a problem like Burger’s equation typically involves the following steps:

1. Neural Network Architecture: A neural network is trained to approximate the solution $u(x,t)$ of the PDE, where the input is the space-time coordinates $(x,t)$, and the output is the predicted solution $u(x,t)$.
2. Physics-Based Loss Function: The neural network is trained not only to fit the initial and boundary conditions but also to minimize the residuals of the governing PDE. For Burger’s equation, this means the network must satisfy the equation:

   ∂u∂t+u∂u∂x−ν∂2u∂x2=0\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} – \nu \frac{\partial^2 u}{\partial x^2} = 0∂t∂u​+u∂x∂u​−ν∂x2∂2u​=0This equation is included as part of the loss function, ensuring that the neural network output respects the underlying physical laws.

3. Handling Discontinuities: PINNs can efficiently handle discontinuities by learning to approximate solutions with sharp transitions. The neural network adjusts its weights to capture the locations of shocks or steep gradients, ensuring that the network provides an accurate representation even in regions of high nonlinearity.
4. Training: The training process involves minimizing both the PDE residuals and any additional boundary or initial conditions. The training algorithm optimizes the network to predict $u(x,t)$ in a way that not only fits the data but also obeys the physics described by Burger’s equation.

Advantages of Using PINNs for Burger’s Equation

1. Accurate Shock Representation: Unlike traditional numerical methods, PINNs are well-suited to capturing sharp gradients and discontinuities, allowing for accurate representation of shock waves without smearing or oscillations.
2. Mesh-Free Approach: PINNs do not require a traditional grid or mesh, which means they avoid the problem of mesh refinement in shock regions. This makes them computationally efficient, especially for large-scale problems.
3. Generalizability: PINNs can be applied to a wide variety of PDEs, not just Burger’s equation. Once trained, the network can be used to solve different problems with similar underlying physics, making it a versatile tool in computational physics.
4. Improved Stability and Precision: By incorporating the governing equations directly into the training process, PINNs can achieve greater stability and precision when compared to traditional methods, even in the presence of sharp discontinuities.

Applications of PINNs in Solving Burger’s Equation

PINNs have been successfully applied to solve Burger’s equation in several areas of research and practical applications:

• Fluid Mechanics: Modeling turbulence and shock waves in compressible fluid dynamics.
• Traffic Flow: Simulating the movement of vehicles in a traffic system, where congestion creates shock-like behaviors.
• Acoustic Waves: Studying shock formation in nonlinear acoustic waves in various media.

In each case, PINNs offer an efficient and accurate method for solving Burger’s equation, even when faced with challenging discontinuities that traditional methods struggle to handle.

Conclusion

Burger’s equation, with its inherent discontinuities, presents a unique challenge to numerical methods in computational physics. However, Physics-Informed Neural Networks (PINNs) have emerged as a powerful tool for overcoming these challenges. By integrating the laws of physics directly into the neural network’s learning process, PINNs can solve PDEs with high accuracy and stability, even in the presence of sharp gradients and shock waves. As machine learning continues to evolve, the potential for PINNs to revolutionize how we solve complex physical problems is immense, offering a promising future for computational science across a range of disciplines.